Topic 1 - Animal Locomotion

1Introduction¶
Imagine a giraffe, a Chihuahua, and an ant walking side by side without undue urgency. For every stride that the giraffe makes, the Chihuahua takes many and the ant many more. Most people intuitively know that the shorter the length of one’s legs, the faster they tend to swing. In other words, an inverse relation exists between the size of a creature and how quickly it can move its legs. Why would such a scaling relation exist?
When walking at a leisurely pace, one may assume that the locomotion is executed in a way that minimizes energy expenditure. A way to accomplish this is to let gravity do as much of the work whenever possible. When an animal takes a step, the leg swings naturally from the hip, much like a pendulum in a gravitational field. If the animal swings them faster or slower than their natural swinging time, you might think this may require undesirable additional energy expenditure. Thus, animals may want to swing their legs at precisely the natural swinging frequency of a pendulum in order to minimize energy expenditure. If so, does this account for why animals with shorter legs tend to swing them at a faster rate? Let us set up the model and find out.
2Pendulum Motion¶
2.1The Simple Pendulum: A Case in Point¶
While almost any object can act as a pendulum, those that possess complex physical forms are difficult to analyze. For this reason, we will begin by examining the most straightforward case: the simple pendulum in a gravitational field. The simple pendulum is aptly named, for it simply consists of a point mass suspended from a massless string. The string is made massless to avoid having to calculate its rotational inertia, which, as you may recall, is a quantity that depends on the distribution of mass. If we think of the leg as a simple pendulum, it is as if the entire mass of the leg is concentrated in the foot. Figure 1 below shows a simple pendulum of length and mass . As the pendulum oscillates, the point mass traces an arc of the circle of radius .
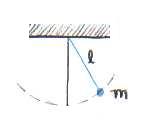
Figure 1:The simple pendulum with length and mass .
We are now ready to derive an equation that describes the position of the pendulum as a function of time. From the equation, we will then obtain another equation that computes the stepping time for an animal.
What are the forces acting on the mass? The best way to visualize them is by drawing a force diagram (Figure 2).
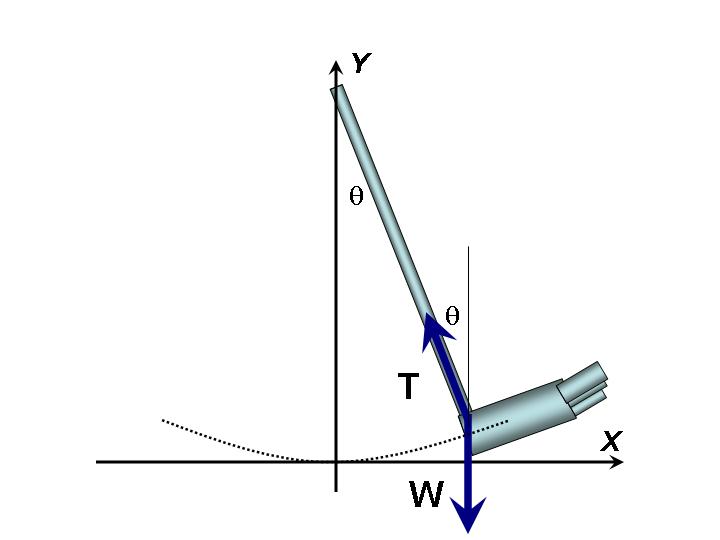
Figure 2:Free-body diagram for mass .
According to Newton’s 2nd Law, the sum of the forces along the -axis and -axis are equal to the mass, , multiplied by the acceleration in the -direction, , and in the -direction, , respectively.
To simplify the problem, we will assume that the movement of the foot along the -direction is always negligible compared to the one along the -direction. This is approximately true when taking moderate steps, for which the angle rarely exceeds 20°. If so, we may also ignore the acceleration of the foot along the when we invoke Newton’s second law. When taking this into account, and breaking down the forces into and components as shown in Figure 3, we obtain
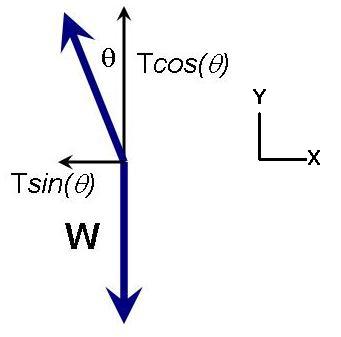
Figure 3:Force diagram, with the tension, , broken down into its and components.
When Eqn. (3) is solved for the tension (), and this expression is substituted for in Eqn. (2), we derive the following relation between and the weight
Since , we can simplify:
Note that the acceleration is not constant, that is, it varies with the angle , which is dependent on the position of the foot along the horizontal. Hence we cannot use simple approaches like the kinematic equations to solve for the time it takes to complete a step. We will approach the solution to Eqn. (5) differently than what is done in an introductory physics course. Recall that the tangent of an angle can be defined as the ratio of the opposite and adjacent sides of a right triangle.
In our case, as shown below in Figure 4, the adjacent of angle is simply the length of the leg .
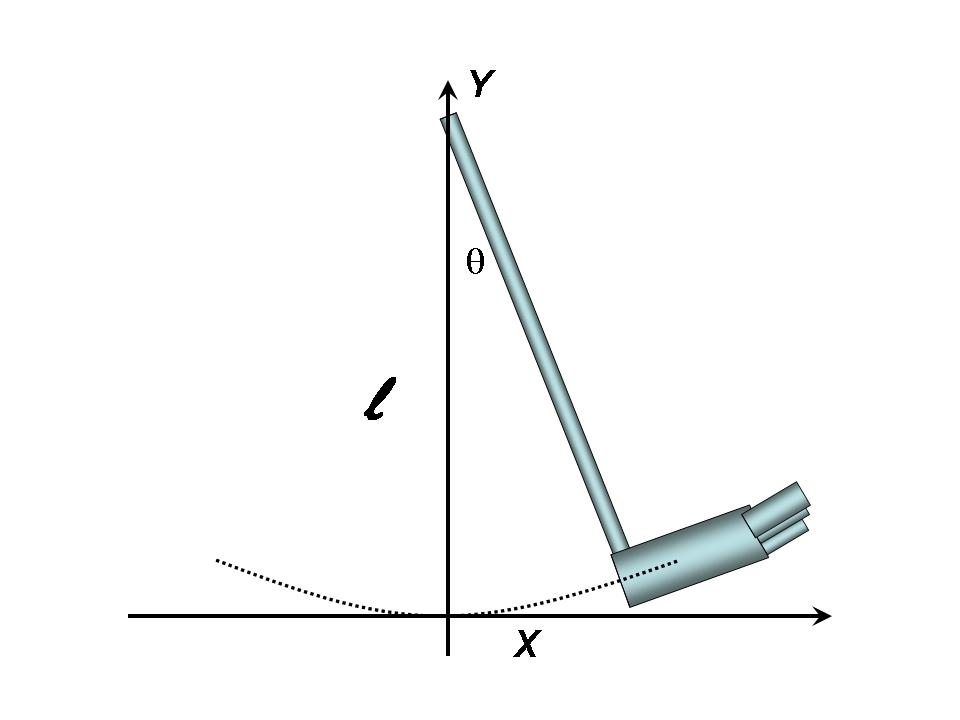
Figure 4:Adjacent and opposite sides of the triangle defined by .
The opposite here corresponds to the displacement of the foot, or , along the x-direction. Accordingly, , and Eqn. (5) becomes:
But also varies with position and time. Recall that velocity is the first derivative of position with respect to time and that acceleration is the first derivative of velocity with respect to time. It follows that acceleration is the second derivative of position with respect to time, written in differential form as:
Substituting Eqn. (7) into Eqn. (8), we arrive at the equation we must solve for :
Eqn.(9) is of a type known as a ``differential equation’’ because it contains a derivative of what you solving for. Since solving differential equations is beyond the scope of the course, the steps are left to the more ambitious student. However, as you will verify in one of your homework problems, the following solutions satisfy Eqn.(9).
where is a constant. [1]
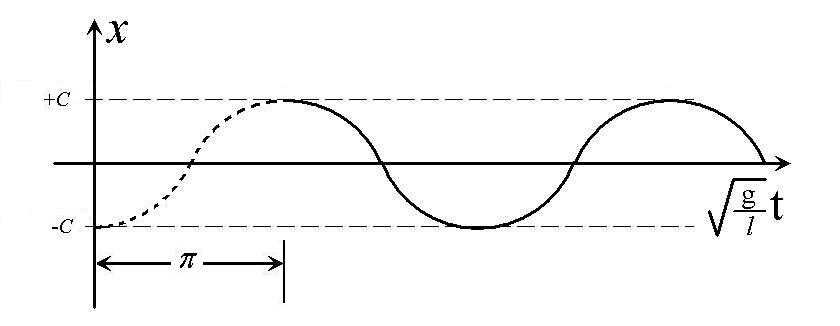
The constant, , in each case refers to the amplitude of the step, and we can visualize the motion in terms of its oscillatory behavior, shown in Figure 5.
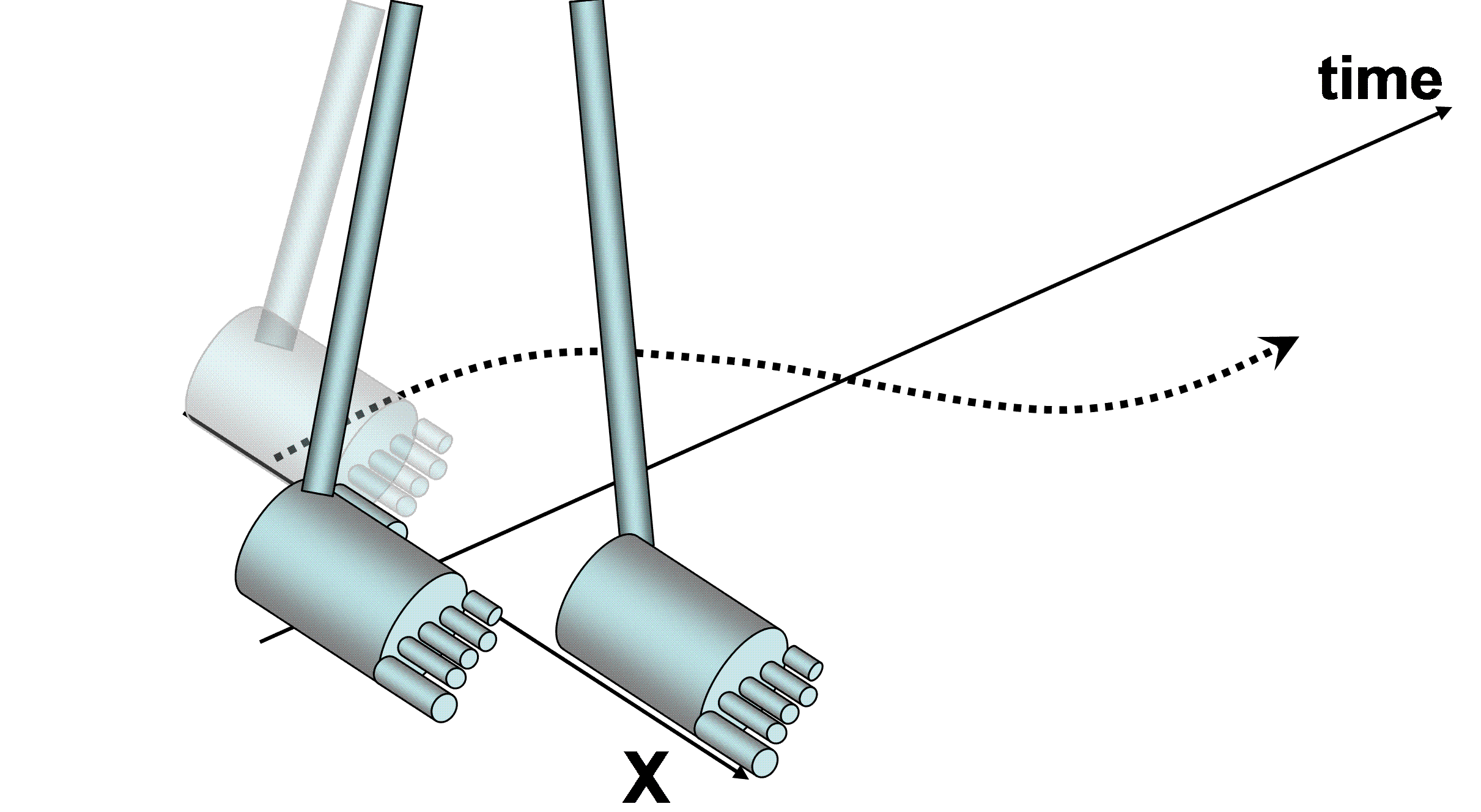
(a)The leg swings forward.
(b)The position of the leg moves through π radians during this interval.
Figure 5:As the back leg moves forward it undergoes motion corresponding to half of a full pendulum oscillation.
From Figure 5 we see that a step corresponds to one half of the full sinusoidal oscillation. In terms of our solutions Eqn. (10), this corresponds to a time such that
Solving for , we get the theoretical time it takes for the leg to step forward:
Interestingly enough, in this model, the mass of the body or leg does not affect how long it takes for an animal to take a step; only the leg length and the magnitude of gravity are determining factors. Note that the stepping time varies with the square root of , proving that our intuition is correct—longer legs do require more time to take a step.
How accurately does Eqn. (12) predict stepping time? The leg of the average adult human is approximately 0.9 m, corresponding to a theoretical stepping time of 0.95 s. Biophysics students measure as part of a laboratory activity, finding it to be closer to 0.6-0.7 s. The error is about 50%, which is relatively small when one considers that the human leg looks nothing like a point mass attached to a massless string. In the next section, we will improve the model by taking into account the distribution of mass in the leg.
2.2The Physical Pendulum: A Refined Model¶
Contrasted with the simple pendulum where the mass is concentrated at a point, the physical pendulum approach is capable of handling any arbitrary distribution of mass that swings about a fixed pivot. Examine the diagram shown below for a human leg swinging as a physical pendulum.
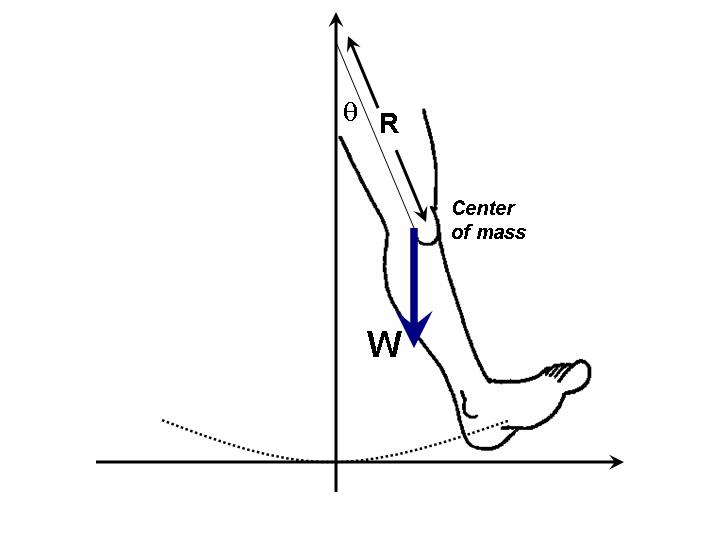
Figure 6:Free body diagram of the physical pendulum.
A significant difference between the simple pendulum and the physical pendulum models is that the first looks at the action of forces, whereas the second focuses on torques. Recall that a torque is the turning force that causes objects to rotate about a pivot point. The strength of the torque is dependent not only on the applied force but also on distance from where it is applied to the pivot point. In this case, gravity is the only force that causes rotational motion, and the magnitude of the torque associated with this force is the force times the distance from where it is applied to the pivot point (). In addition, the product must be multiplied by the sine of the angle between the directions of the force and the line of action which connects the pivot point to the center of mass. The resulting expression is , or , where is the distance from the pivot point to the center of mass. Note that in Figure 6 the direction of the torque (clockwise) opposes the angular displacement (counter-clokwise). This is always the case, even if the leg is to the left of the centerline; in that case the direction of the angular displacement is clockwise whereas that of the torque is counter-clockwise. The sum of the torques acting on the mass obeys the equation
where is now defining torque rather than a characteristice time, is the moment of inertia and is the angular acceleration. Recall that the moment of inertia takes into account the distribution of mass of the leg. In fact, if you divide the leg into small masses, and identify each mass with an index , the moment of inertia is given by the formula
Angular acceleration, is the second derivative of with respect to time. Thus, Eqn.(13) can be rewritten as
Rearranging, we get:
As we stated earlier, an animal’s leg rarely subtends an angle greater than 20° relative to the normal while walking. This means that that we can take advantage of the small angle approximation, which states that for angles less than 20°, . (Recall that the small angle approximation only holds when the angle is expressed in radians.) Eqn.(16) simplifies to
Compare Eqn. (9) to Eqn. (17). Instead of , we now have , and instead of the constant , we now have . Observing these substitutions makes solving Eqn. (17) easy, because we have already solved Eqn. (9). The solutions are of the form:
Also analogous to the previous case, a step corresponds to the time when the period is
and the stepping time is
As stated above, the moment of inertia of an object pivoting about an axis is found by first breaking down the object into small pieces each with the same mass . After identifying each mass with an index , the moment of inertia is given by the formula . Most physics textbooks list the result of this calculation for the moments of inertia of various bodies with simple geometries. To take advantage of these existing formulas for , we can assume a simplified shape for the leg by thinking of it as a slender rod with a pivot through one end (the hip). Accordingly,
where is the length of the leg and is the total mass of the leg. If we substitute these equations into Eqn. (20), we get an equation that calculates the stepping time, accounting for the continuous mass distribution of the leg.
This equation is almost identical to Eqn.(12) for the simple pendulum case, with the exception of a new constant, , which is approximately 0.8. The new factor makes the theoretical stepping time = 0.78 s, which is about 20% lower than when computed using the simple pendulum model. Now, the theoretical time more closely matches the experimental measurements for adult humans, which was in the range of 0.6 to 0.7 s.
One might be tempted to think that leg length is the only variable that affects the stepping time. However, is just as dependent on the gravitational constant. Eqn. (22) explains why astronauts move differently on the moon, where is about 1/6 of Earth’s value. Because of the diminished , each step takes about 2.5 (or ) times as long as on Earth. The increased stepping time apparently became unbearably long for these astronauts, who immediately found that to get from point A to point B quickly, it was more efficient to hop than to walk. This incident also underscores how our bodies have adapted to the gravitational environment in which we live.
3Problems¶
Verify that the solutions for given by Eqn. (10) satisfy equation (9).
T. Rex legs have been measured to be 2.5 m long.
a. Estimate the stepping time for this animal.
b. Assuming that the angular displacement of the leg is ±100, estimate the distance covered during a single step.
c. from (a) and (b) estimate the walking speed of this animal in miles per hour. Could you outrun a T. Rex under these conditions?
Fill in missing algebraic steps to get from Eqn. (18) to (22) in the text.
Much of the theoretical work done in class was based on the small angle approximation, which assumed that for angles smaller than the following applied:
Calculate the percent error for angles from to (in steps of ) to demonstrate the validity of the above approximation. Note: the approximation for works only when the angle is expressed in radians. You should also show that this is true.
Imagine that in the distant future some humans will have colonized planets with high gravity environments for millions of years and will have evolved to adapt to them. Speculate on whether their legs will be shorter or longer then. (Note: there is no single correct answer to this question but you must provide a plausible argument to support it).