Now that you have some familiarity with velocity and acceleration, we can introduce the idea of the total force on an object which is in motion. The action of forces is the means by which energy is transferred between objects so it will be very important for our later discussions. We start with a situation in which there is very little friction impeding the motion of the object. For example consider ice skating. Suppose you are standing at the edge of a skating rink and give your little brother (weighs 50 pounds, on skates) a push while holding on to the rail. He goes flying off at some speed. Now suppose you give your sister (100 pounds) an identical push. It turns out that if you measure the final speed of both family members, the little brother will be going twice as fast. We say for a given force on the object (the push which you gave) the acceleration is less if the object has more mass.
Here we write mass instead of weight. Mass is closely related to weight but it is not quite the same. In the example, the mass of the brother and sister is proportional to the weight. To make a determination of the mass of an object, the most conceptually straight forward way is to use a set of standard masses and a balance. The mass of the object is then the amount of standard mass required for balancing the mass of the object.
Now if you look at the word equation above you see that you know how to measure acceleration (from last weekʹs experiments) and we just discussed how to measure mass, so the only thing left in the equation is the total force. So you can turn the equation around by multiplying by mass to solve for the total force:
This famous equation, often written , is Newtonʹs second law of motion. So far it basically just defines what we mean by the total force on an object. It becomes useful if we have some additional information about the force. For example consider an object dropped so that it falls straight down. You probably heard that Galileo made experiments with dropping objects and found out that massive balls falling from the top of the leaning tower of Pisa hit the ground at the same time as much less massive ones dropped at the same time. This is interpreted to mean that the acceleration of the balls is the same whether they have a lot of mass or a little mass. But now look at the equation . The only way it can be true in the case of the falling objects is if the gravitational force on a falling object increases with its mass. Suppose that is true, say that where is some constant acceleration due to gravity. Substituting this back in Newtonʹs second law we get
so , that is the acceleration of falling objects is independent of mass, as Galileo(and many others) observed. So from Newtonʹs second law plus an experiment we learned something about gravitational forces, namely that they are proportional to the mass in the moving object. But not all forces in nature have this property of being proportional to the mass in the object. For example the push that you give your sister or brother is not a gravitational force. It is generated by your muscles and which act through what are called electromagnetic forces in physics. That is why, when you push them, the little brother ends up going faster than the sister, but if you dropped them off a bridge (of course you wouldnʹt do that) they would both accelerate the same amount. Most of the time in this course, the forces we consider will be gravitational or electromagnetic in origin. These are two of the four main categories of force known to physicists. At the end of the course we will consider another one dsof the four kinds, nuclear force.
In applying Newtonʹs second law, it is often important to keep in mind that it refers to the total force on an object and that this total can be the combined result of the action of more than one kind of force. Furthermore, these different forces are not always acting in the same direction and can partially or completely cancel each other out. As an example, suppose you hold a book out in front of you over the floor. As you hold it there, it is not accelerating so the total force on it is zero by Newtonʹs second law. But the force of gravity is pulling down on it and you are pushing up on it with your hand (with a force that is electromagnetic in origin). The two forces are exactly equal in magnitude but opposite in direction and cancel each other exactly as long as the book doesnʹt fall.
In more complicated cases, forces, again ultimately of electromagnetic origin, of friction and air resistance play a role. These more complicated cases (which made the early study of the subject in past centuries difficult) will be discussed later. In this laboratory you will consider cases in which they can be neglected. You and your partners will measure the velocity and the acceleration of an object to understand how it obeys Newtonʹs second law.
Pre‐lab reading¶
Textbook Chapter 5.2 on Dynamics
Equipment¶
1 aluminum track
1 metric ruler on the track
1 mass hanger
1 mass set
1 low friction PASCO cart
1 piece of string
1 computer with Capstone
Predictions/preliminary questions¶
Sketch a graph of velocity vs. time for a cart used in lab, moving with a constant velocity.
Sketch a graph of velocity vs. time for a low friction cart that is moving down an incline.
On the same graph as question #2, sketch a graph of velocity vs time for a cart that is about twice as heavy and is moving on the same incline as the cart in question #2.
You are welcome to test your prediction if you’d like.
Sketch a graph of velocity vs. time for a cart moving on a horizontal track being pulled by a weight that is connected by a string over a pulley. (See Figure 1.)
Sketch a graph of velocity vs. time for the same cart with extra mass attached (so the total mass of the cart and added mass is about twice the mass of the cart alone). The cart with extra mass is being pulled by the same weight as in question #4. Put the sketch on the same graph as question #4.
Procedure¶
There are two situations. The first involves an inclined track (Part 1), and the second involves a level track with a hanging mass pulling the cart (Part 2) In both exercises below, mass will be added to the low‐friction cart for an additional trial.
Part 1: inclined track, cart¶
Use a low friction PASCO cart. Raise one end of the aluminum track to make the incline as we did in Lab 1 - Velocity and Acceleration.
First discuss with your partner(s) and make a prediction: How would you expect a velocity vs. time graph to look for a cart on an incline? Draw a sketch of the graph for velocity vs. time.
Using the track ruler and stopwatch to determine the average velocity of the cart on the incline. This is total distance divided by total time of travel.
Using the computer and motion sensing cart:
a) Obtain a distance vs. time graph for the cart on the incline.
b) Obtain a velocity vs. time graph
c) How can you obtain the acceleration for the cart from the velocity vs. time graph?
d) What is the acceleration of the cart?
e) Is the acceleration increasing, decreasing, or constant? How can you tell?
Now add 250 g to the cart. This approximately doubles the mass of the cart Record the approximate mass of the cart and the approximate mass that you add to the cart. Repeat step #3. How does the acceleration this time compare with the acceleration without extra mass? Explain your results in terms of Newton’s 2nd Law.
Part 2: tension and level track¶
Level the track such that the cart can be put anywhere on the track, and it does not move. Attach a string to the cart, hang it over a pulley, and tie a mass to the other end (This mass is labeled “A” in Figure 1). Now the cart is free to move in the horizontal direction, and the only unbalanced force on it is the tension in the string from the weight hanging off the end. You and your partners will find the cart’s acceleration due to this tension.
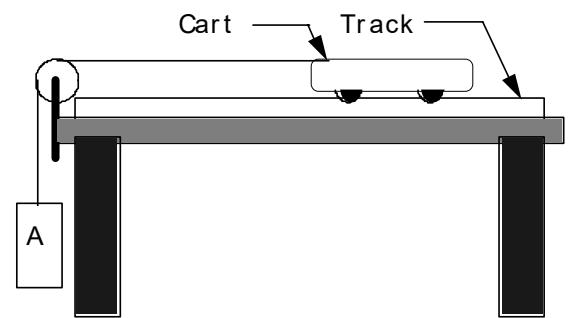
Figure 1:Cart on a level track pulled by a mass falling due to gravity.
Using the computer and motion sensor:
a) Obtain a distance vs. time graph for the cart accelerating (before the hanging mass hits the floor.)
b) Obtain a velocity vs. time graph for the cart.
c) How can you obtain the acceleration for the cart from the velocity vs. time graph?
d) What is the acceleration?
e) Is the acceleration increasing, decreasing, or constant? How can you tell?
Now add additional 250 g of mass to the cart. Repeat your data collection with the more massive cart in order to calculate its acceleration. What is the acceleration of the more massive cart? How does it compare to the earlier acceleration? If you assume that the tension in the string is the same in the two experiments, what does Newtonʹs second law tell you about what how the two measured accelerations should be related?
Conclusions¶
a) Did the low-friction cart in Part 1 accelerate as it moved down the incline? How do you know?
b) Was the acceleration of the more massive cart greater than, less than, or equal to the acceleration of the cart with no additional mass?
c) When more mass was added to the cart, did the total force on the cart change? Did the acceleration change? Explain how your observations do or do not agree with Newton’s second law of motion.
a) Did the low‐friction cart in Part 2 accelerate as it moved down the incline? How do you know?
b) Was the acceleration of the more massive cart greater than, less than, or equal to the acceleration of the cart with no additional mass?
c) When more mass was added to the cart, did the total force on the cart change? Did the acceleration change? Explain how your observations do or do not agree with Newton’s second law of motion.
a) Compare what happened to the acceleration in Part I and Part II when more mass was added to the cart (refer to your answers for questions 1b and 2b.)
b) Compare what happened to the force in Part I and Part II when more mass was added to the cart.
c) If there are differences between Parts I and II, what are they? If there are no differences, how are these trials the same?
Newtonʹs second law of motion is one of the most fundamental relationships of all physics. Together with conservation of energy, it forms the basis of all Newtonian physics. It is hard to exaggerate the importance of Newtonʹs second law when it can be applied in a wide range of topics, from projectile motion to electromagnetic fields. It was the concept of force that was essential to the development of mechanics and all physics. Be certain you can identify the specific forces acting in both parts of this laboratory.
Historical notes¶
You should not be embarrassed if you find it a little tricky to sort out what is happening in the motion of these simple objects. Though the concepts of acceleration, velocity, force and Newtonʹs second law are quite simple to state, very intelligent people studied these questions for thousands of years before finally getting them right. For example early (more than 2500 years ago) Greek natural philosophers, such as Thales, Anaximander, and Anaximenes, thought that motion was eternal and somehow contained ʺinsideʺ all things. Aristotle, who wrote a book called ʹPhysicsʹ that was widely used in Europe during the Middle Ages, thought that rest is the natural condition of objects and that there are two types of motion ‐‐ ʺnatural motionʺ is due to an objectʹs natural tendency towards its proper place where it then rests, and ʺunnatural motionʺ is caused by something other than the object itself. At a similar time (900s AD), Ibn al-Haytham developed models of inertia and motion that were close to Newton’s first and second laws. It was not until the work of Galileo, who died about 360 years ago, that forces and acceleration started to be correctly understood. A major difference between Galileo and his predecessors is that Galileo did not just think about motion. He did experiments much like the ones you have done in this laboratory.